type
status
date
slug
summary
tags
category
icon
password
Description
监督式机器学习算法详解
监督式学习算法堪称众多机器学习（ML）项目的核心基础，它让计算机系统能够通过已标注的数据集进行学习，并输出精准的预测结果。在这种学习模式下，每一个数据样本都配有对应的正确答案或标签——简单来说，就像是给AI一套"标准答案"让它参考学习。
该类算法的核心目标是构建一个映射函数，用以对从未见过的全新数据进行标签预测。整个过程需要识别输入变量（特征）与输出变量（标签）之间的内在规律和关联性，让算法能够将习得的知识泛化应用到崭新的实例当中。
监督学习的工作机制
不妨这样想象：当你教导小朋友区分各种水果时，会先展示一个苹果并告诉他们"这个是苹果"，接着展示橙子说"这个是橙子"。通过不断展示这些带有标签的实例，小朋友逐渐掌握了根据颜色、形状、尺寸等特征来辨识不同水果的能力。
监督学习算法的运作原理与此如出一辙——它们接收包含大量已标注样本的数据集作为输入，利用这些数据训练出一个模型，该模型具备对全新、未知样本进行标签预测的能力。整个训练流程涉及调优模型参数，让预测输出与真实标签之间的偏差降到最低。（比如早期的TensorFlow图像识别模型就是典型案例）
监督式学习任务通常可以划分为两个主要类别：
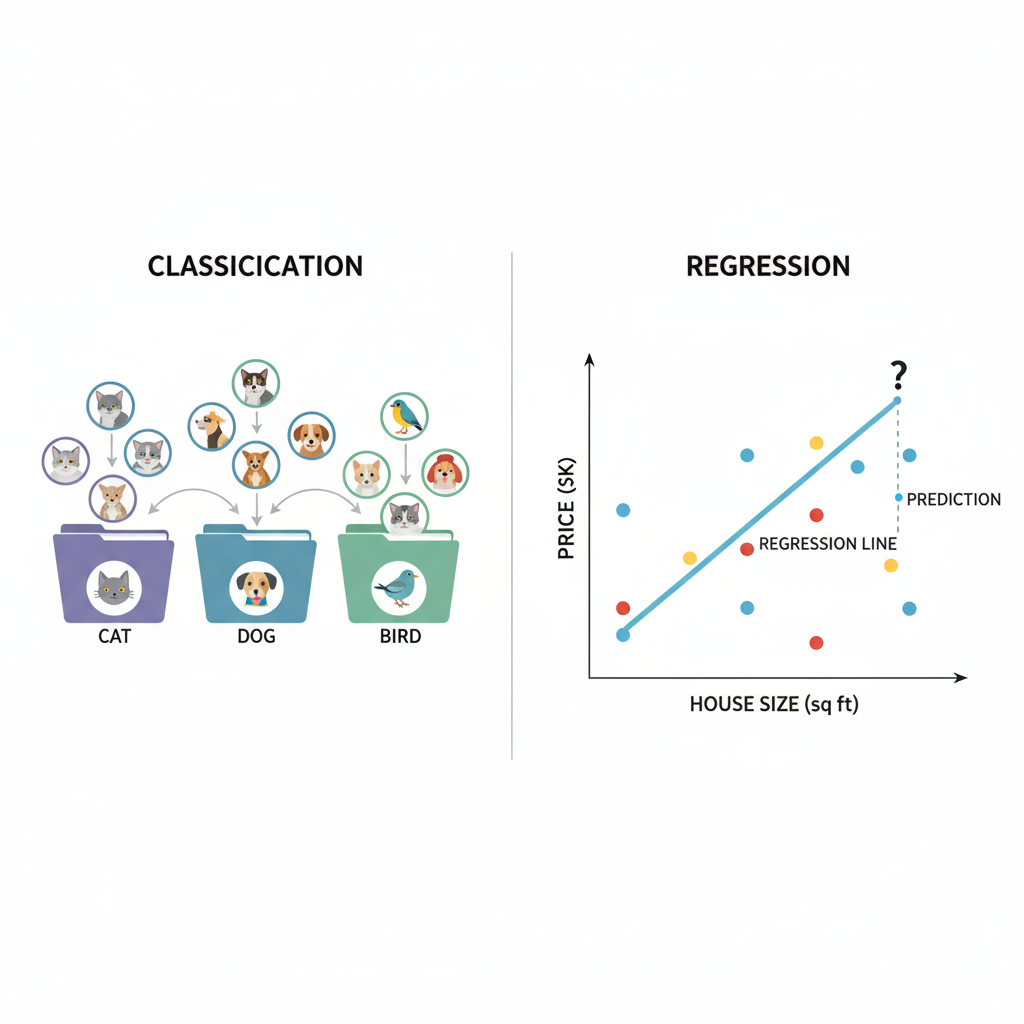
分类任务：这类问题的目标是预测离散的类别标签。举例来说，判断邮件是否为垃圾邮件，或者识别图像中的动物是猫、狗还是鸟。
回归任务：这类问题要求预测连续数值。比如基于房屋面积、地理位置等特征预测房价，或者预测股市走势。
监督学习的关键概念解析
掌握监督学习的核心理念对于深入理解该领域至关重要。这些概念构成了理解算法如何从带标签数据中学习并产出准确预测的理论基石。
训练数据集
训练数据集是监督学习的根基所在。它指的是用来训练机器学习模型的已标注数据集合。该数据集由输入特征及其对应的输出标签构成。训练数据的品质和规模直接影响模型的准确性以及对新数据的泛化表现。
可以将训练数据集想象成一套附带标准答案的练习题。算法通过学习这些实例，开发出一个能够解决类似问题的模型。
举个实际例子：在进行渗透测试的过程中，暴力破解密码时常常遇到验证码阻拦，这时候一个训练得当的识别模型就显得非常重要了。当然近年来验证码的形式愈发复杂，这正是攻防技术不断升级的对抗博弈过程。
特征工程
特征指的是作为模型输入的数据可测量属性或特性。它们是算法用于学习和预测的变量。选择合适的特征对构建高效模型来说至关重要。
以房价预测为例，特征可能涵盖：
- 建筑面积
- 卧室数目
- 所在位置
- 建筑年限
标签定义
标签表示训练集中每个数据点关联的已知结果或目标变量。它们代表模型期望预测的"标准答案"。
在房价预测模型示例中，标签就是房屋的实际售价。
模型构建
模型是特征与标签之间关系的数学表征。它从训练数据中获得知识，并用于对新的、未知数据进行预测。可以把模型理解为一个函数，接受特征作为输入，输出对标签的预测结果。
预测过程
模型训练完毕后，就能用它对新的、未知数据进行预测。这个过程涉及向模型提供新数据点的特征，模型随后输出对标签的预测。预测是推理的具体应用，专注于生成可执行的输出，比如将邮件归类为垃圾邮件或预测股价（A股除外哈）。
推理分析
推理是一个更宽泛的概念，不仅涵盖预测，还包括理解数据中的潜在结构和规律。它涉及使用经过训练的模型来获取洞察、估算参数并理解变量间的关联。
比如，推理可能包括确定决策树中最关键的特征，估算线性回归模型的系数，或分析不同输入如何影响模型预测。预测强调可操作的输出成果，而推理更多聚焦于解释和阐释结果。
性能评估
评估是监督学习流程中的关键环节。它涉及评价模型表现，以确定其准确性和对新数据的泛化能力。常用的评估指标包括：
- 准确率：模型预测正确的比例
- 精准率：真正例预测在所有正例预测中的占比
- 召回率：在所有实际正例实例中，真正例预测的比例
- F1得分：精准率和召回率的调和均值，提供模型性能的平衡度量
泛化能力
泛化指模型对训练阶段未接触过的新数据进行准确预测的能力。泛化能力出众的模型能够有效地将学到的知识应用到现实场景中。
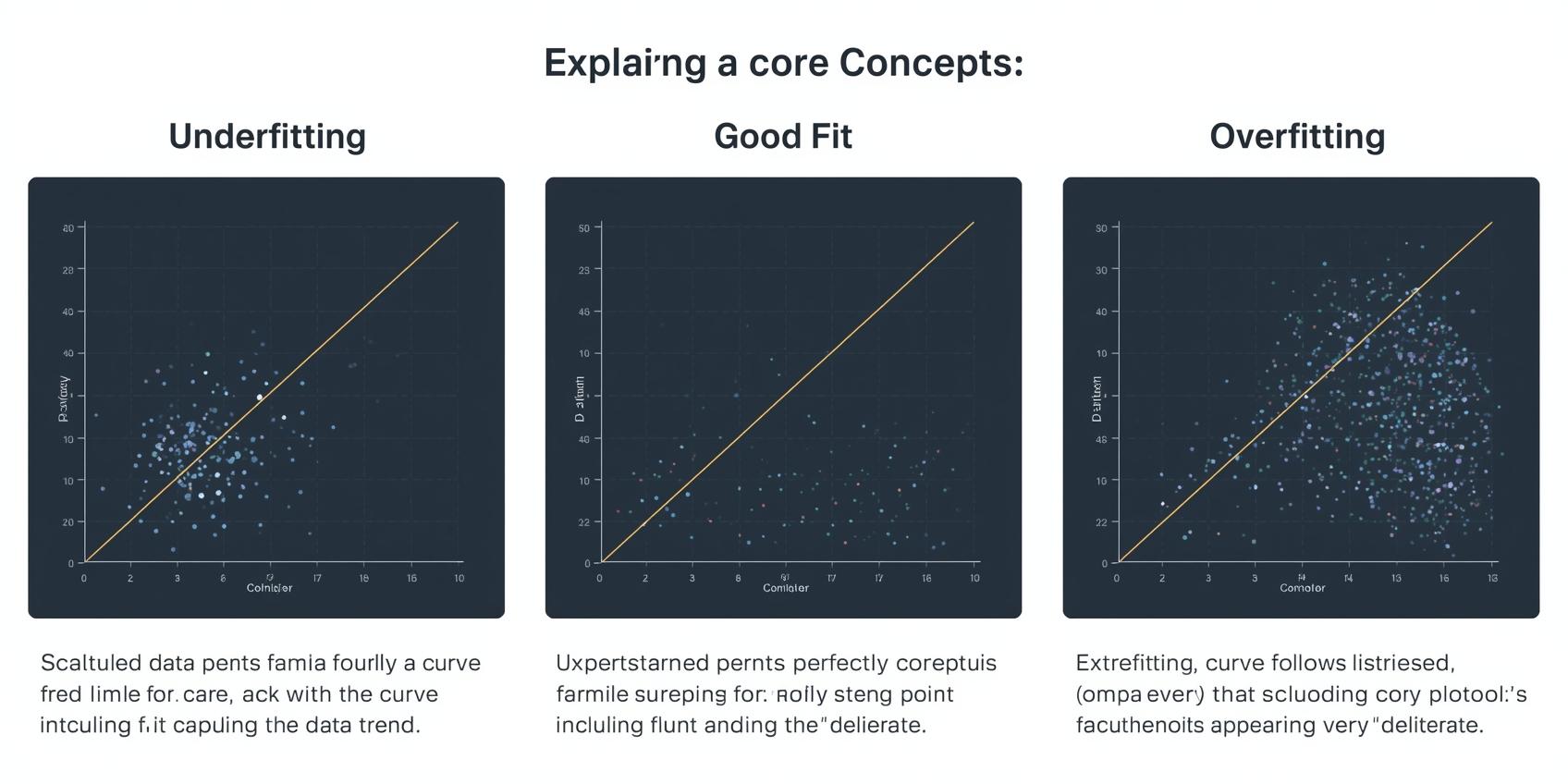
过度拟合
当模型对训练数据（包括噪声和异常点）学习得过于充分时，就会发生过度拟合现象。这可能导致对新数据的泛化表现不理想，因为模型记住了训练集，而非学习基本规律。
拟合不足
拟合不足指模型过于简化，无法捕获数据中的基本模式。这会导致在训练数据和未见过的新数据上都表现不佳。
交叉验证技术
交叉验证是一种评估模型对独立数据集泛化程度的方法。它包括将数据分割成多个子集（折叠），在这些折叠的不同组合上训练模型，同时在剩余折叠上验证模型。这有助于减少过度拟合，并对模型性能做出更可靠的估计。
正则化方法
正则化技术在机器学习中是防止模型过度拟合的重要手段，它通过在损失函数中加入惩罚项，这种惩罚机制会阻止模型学习过于复杂的模式，从而限制模型的学习能力，使模型具备更好的泛化性能。常见的正则化技术包括：
- L2正则化：加入等于系数平方的惩罚项
- L1正则化：加入等于系数绝对值的惩罚项
关于过度拟合的一点经验分享：在基于知识库微调大语言模型时（俗称炼丹），经常会碰到过度拟合的情况。
线性回归算法详解
线性回归是一种基础的监督学习算法，它通过在目标变量与一个或多个预测变量之间构建线性关系来预测连续的目标变量。该算法采用线性方程对这种关系进行建模，其中预测变量的变化会引起目标变量成比例的变化。目标是寻找最优拟合直线，以最小化预测值与实际值之间平方差的总和。
想象这样一个场景：你尝试根据房屋面积来预测其售价。线性回归试图找到一条最能体现这两个变量间关系的直线。随着房屋面积增大，价格通常也会上涨。线性回归量化了这种关联性，使我们能够基于房屋面积预测房价。
回归分析的本质
在深入探讨线性回归之前，有必要先理解机器学习中回归分析的宽泛概念。回归分析是监督学习的一种类型，其目标是预测一个连续的目标变量。这个目标变量可以在给定范围内取任意数值。可以把它想象成估算一个具体数字，而非将事物分类到不同类别中（这正是分类算法的功能）。
回归问题的典型例子包括：
- 基于房屋面积、位置和房龄预测房价
- 根据历史气象数据预测每日温度
- 基于营销投入和时间估算网站访问量
在所有这些情况下，我们试图预测的输出都是连续数值。这正是回归与分类的根本差异，分类的输出是分类标签（例如"垃圾邮件"或"正常邮件"）。
现在，明确了这一点后，让我们重新审视线性回归。这仅仅是回归分析的一种特定形式，我们假设预测变量和目标变量之间存在线性关系。这意味着我们试图用一条直线来建模这种关系。
一元线性回归
在最基础的形式中，一元线性回归涉及一个预测变量和一个目标变量。用线性方程表示它们的关系：
y是预测的目标变量
x是预测变量
m是直线斜率（表示x和y之间的关系强度）
c是y轴截距（当x为0时y的取值）
简单描述：一元函数关系
该算法旨在找到m和c的最优值，使训练数据中预测y值与实际y值之间的误差最小。这通常通过普通最小二乘法(OLS)来实现，其目的是最小化误差平方和。
多元线性回归
当涉及多个预测变量时，就叫做多元线性回归。方程变为：
y是预测的目标变量
x1,x2, …,xn是各个预测变量
b0为y轴截距
b1、b2、…、bn是表示各预测变量与目标变量关系的系数
简单描述：多元函数关系
普通最小二乘法原理
Scatter plot with data points, a linear regression line, and residuals labeled 'Linear Regression with Residuals
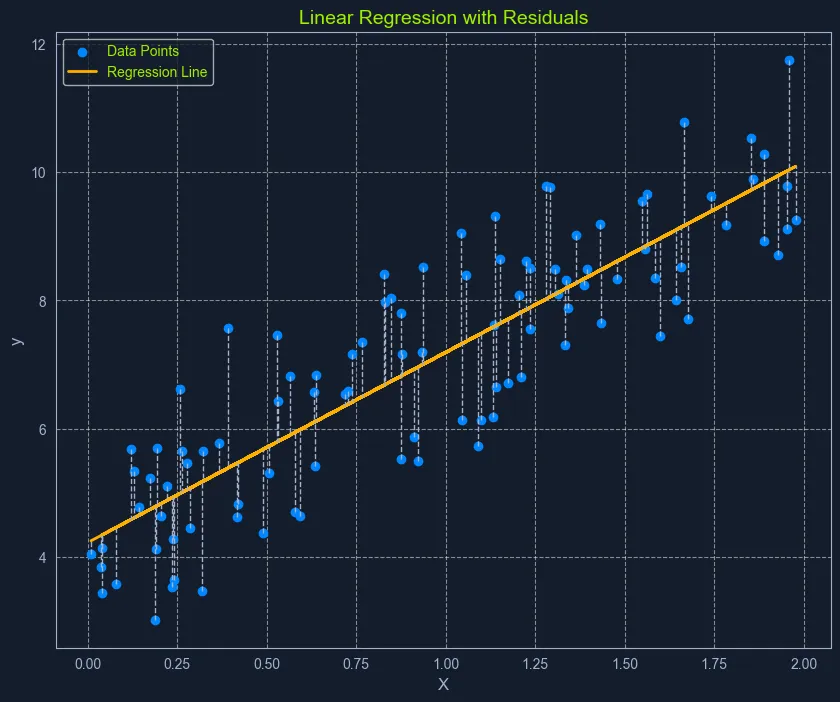
普通最小二乘法（OLS）是估计线性回归中系数最优值的常用方法。它的目标是最小化实际值与模型预测值之间的平方差总和。
可以把它想象成寻找一条直线，使数据点到直线距离形成的正方形总面积最小。这条"最佳拟合线"代表了最能描述数据关系的直线。
以下是OLS过程的详细步骤：
- 计算残差：针对每个数据点，残差是实际y值与模型预测y值的差值
- 残差平方化：将每个残差进行平方处理，确保所有数值为正，并对较大误差赋予更多权重
- 残差平方和：将所有平方残差相加，得到代表模型整体误差的数值。这个总和称为残差平方和（RSS）
- 最小化平方残差和：算法调整系数，寻找使残差平方和（RSS）最小的数值
这个过程可以直观理解为寻找一条直线，使数据点到直线距离形成的正方形总面积达到最小。
线性回归的基本假设
线性回归依赖于数据的几个核心假设：
- 线性关系：预测变量与目标变量之间存在线性关系
- 独立性：数据集中的观测值相互独立
- 同方差性：误差的方差在预测变量的所有水平上保持恒定。这意味着在预测值范围内，残差的分散程度应该基本一致
- 正态性：误差服从正态分布。这个假设对于有效推断模型系数非常关键
在应用线性回归前评估这些假设能确保模型的有效性和可靠性。如果违反这些假设，模型的预测可能不准确或存在误导性。
