type
status
date
slug
summary
tags
category
icon
password
Description
朴素贝叶斯算法深入解析
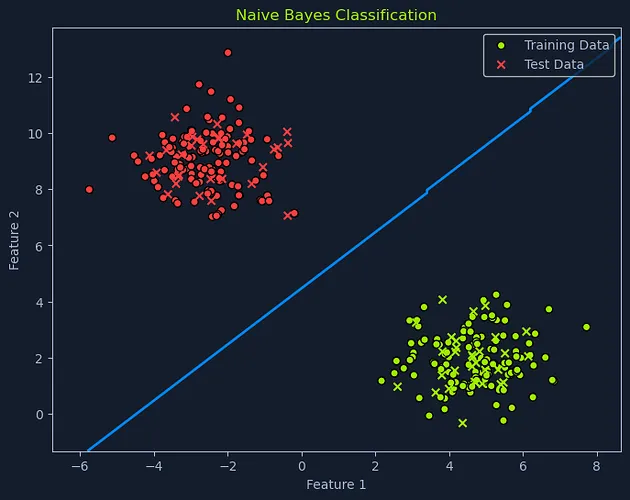
朴素贝叶斯算法是一种基于概率的分类方法，专门用于处理分类问题。该算法建立在贝叶斯定理这一概率论基础概念之上，这个定理描述了如何基于先验知识和观察到的证据来计算事件发生的概率。由于其简洁性、高效性以及在现实应用中令人意外的优异表现，朴素贝叶斯在垃圾邮件过滤、情感分析等任务中备受青睐。
贝叶斯定理核心原理
在深入研究朴素贝叶斯之前，咱们先来理解其理论基石：贝叶斯定理。这个定理为我们提供了一种基于新证据来更新对某事件信念的方法。它让我们能够在另一个事件已经发生的前提下，计算该事件的发生概率。
用数学公式表达为：
- P(A|B)：在事件B已经发生的条件下，事件A发生的后验概率
- P(B|A)：在事件A已经发生的条件下，事件B发生的似然度
- P(A)：事件A发生的先验概率
- P(B)：事件B发生的先验概率
设想我们想知道某人在疾病检测呈阳性（B）的情况下真正患病（A）的概率。贝叶斯定理让我们能够利用该疾病在人群中的先验发病率（P(A)）、患病者检测呈阳性的似然度（P(B|A)）以及检测呈阳性的总概率（P(B)）来计算这个概率。
假设我们掌握以下信息：
- 该疾病在人群中的发病率为1%，所以P(A) = 0.01
- 该检测的准确率为95%，即如果某人患病，有95%的概率检测呈阳性，因此P(B|A) = 0.95
- 检测的假阳性率为5%，即健康人群中有5%的人会检测呈阳性
- 检测呈阳性的概率P(B)，可以通过全概率定律来计算
首先，让我们计算P(B)：
- P(¬A)：未患病的概率，即1 - P(A) = 0.99
- P(B|¬A)：健康人群中检测呈阳性的概率，即假阳性率0.05
现在，代入数值：
接下来，我们运用贝叶斯定理计算P(A|B)：
因此，如果某人检测呈阳性，其真正患病的概率约为16.1%。
这个例子完美展示了贝叶斯定理如何基于新证据来更新我们对事件可能性的认知。在这个案例中，尽管检测相当准确，但由于疾病的低流行率，阳性检测结果实际表明疾病存在的概率仍然相对较低。
朴素贝叶斯运作机制
朴素贝叶斯分类器运用贝叶斯定理来预测某个数据点在给定特征条件下归属于特定类别的概率。为了实现这一目标，它"天真"地假设各特征之间的条件独立性。这意味着，在已知类别标签的情况下，它假设某个特征的存在与否不会影响其他任何特征的存在与否。
让我们来解析一下具体的操作步骤：
计算先验概率：算法首先计算每个类别的先验概率。这是在考虑数据特征之前，数据点属于特定类别的概率。比如，在垃圾邮件检测场景中，邮件是垃圾邮件的概率可能是0.2（20%），而非垃圾邮件的概率是0.8（80%）。
计算似然度：接下来，算法会计算在每个类别下观察到各个特征的似然度。这包括确定在数据点属于特定类别的情况下看到特定特征值的概率。举例来说，如果邮件是垃圾邮件，在邮件中看到"免费"一词的似然度有多大？如果不是垃圾邮件，看到"会议"一词的似然度又如何？
应用贝叶斯定理：对于新的数据点，算法会使用贝叶斯定理将先验概率和似然度结合起来，计算出该数据点属于各个类别的后验概率。后验概率是在考虑了新信息（观察到的特征）后，事件（在此情况下，数据点属于某个类别）的更新概率。这代表了在考虑观察到的特征后，对类别标签的修正信念。
预测类别：最终，算法会将数据点分配给后验概率最高的类别。
尽管在现实数据中，特征独立性的假设往往被违反（比如，"免费"和"优惠"这样的词在垃圾邮件中确实更可能同时出现），但在实际应用中，朴素贝叶斯通常表现得相当不错。就像早期TensorFlow图像识别模型那样，在实际场景中展现出令人意外的效果。
朴素贝叶斯分类器的变体
朴素贝叶斯的具体实现方式取决于特征类型及其假定的分布：
- 高斯朴素贝叶斯：当特征是连续型且假设服从高斯分布（正态分布，钟形曲线）时使用。例如，如果要根据客户的年龄和收入预测其购买行为，可以使用高斯朴素贝叶斯，假设年龄和收入都符合正态分布。
- 多项式朴素贝叶斯：适用于离散特征，常用于文本分类任务。比如在垃圾邮件过滤中，"免费"或"金钱"等词汇的出现频率可能是特征，多项式朴素贝叶斯会建模这些词语在垃圾邮件和正常邮件中出现的概率。
- 伯努利朴素贝叶斯：这种类型适用于二元特征，特征要么存在，要么不存在。在文档分类中，特征可能是特定单词是否出现在文档中。伯努利朴素贝叶斯会建模每个类别中存在或不存在的概率。
选择哪种朴素贝叶斯变体取决于数据的性质和需要解决的具体问题。
数据前提假设
虽然朴素贝叶斯相对鲁棒，但了解一些数据假设仍然很有帮助：
- 特征独立性：如前所述，核心假设是给定类别下的特征是条件独立的
- 数据分布：朴素贝叶斯分类器（高斯、多项式、伯努利）的选择取决于假定的特征分布
- 充足的训练数据：尽管朴素贝叶斯可以使用有限数据，但拥有足够数据来准确估计概率仍然至关重要
支持向量机(SVM)算法详解
支持向量机（SVM）是一种功能强大的监督学习算法，既适用于分类任务也适用于回归任务。它们在处理高维数据以及特征与目标变量之间复杂的非线性关系时表现尤为出色。SVM的目标是寻找最优的超平面，最大化地分离不同类别或拟合回归数据。
SVM的核心思想是找到使边距最大化的超平面。边距是超平面与每个类别最近数据点之间的距离。这些最近的数据点被称为支持向量，它们对于定义超平面和边距起着关键作用。
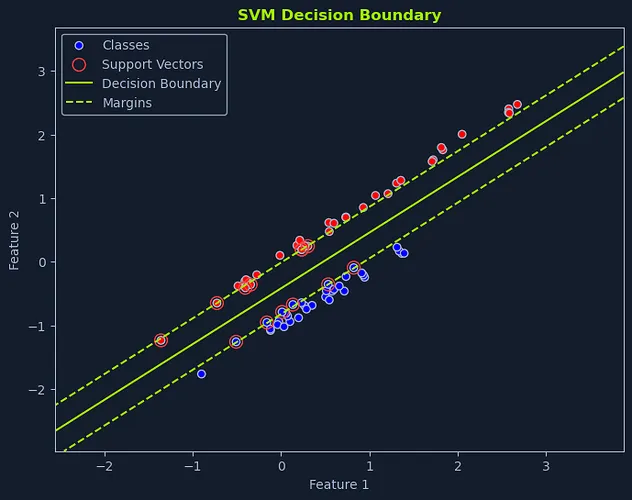
线性SVM详解
线性SVM适用于数据可线性分离的情况，意味着一条直线或超平面能够完美地分离不同类别。我们的目标是寻找最优超平面，在正确分类所有训练数据点的同时，使边距最大化。
寻找最佳超平面
想象一下，你的任务是根据"免费"和"金钱"这两个词的出现频率，将邮件分为垃圾邮件和正常邮件。如果我们将每封邮件绘制在图表上，X轴表示"免费"的频率，Y轴表示"金钱"的频率，我们就能直观地理解SVM的工作原理。
最佳超平面是使不同类别最近数据点之间的边距最大化的超平面。这个边距称为分离超平面。最接近超平面的数据点被称为支持向量，因为它们"支撑"或定义了超平面和边距。
最大化边距的目的是创建一个稳健的分类器。较大的边距使SVM能够在不误判数据点的情况下容忍数据中的一些噪声或变异性。它还能增强模型的泛化能力，使其更可能在未见过的数据上表现出色。
在图表描述的垃圾邮件分类场景中，线性SVM识别出使最近的垃圾邮件与正常邮件之间距离最大化的直线。这条直线是对新邮件进行分类的决策边界。位于该线一侧的邮件被归类为垃圾邮件，位于另一侧的邮件则被归类为正常邮件。
超平面由以下等式定义：
w是权重向量，垂直于超平面
x是输入特征向量
b是偏置项，它使超平面相对于原点发生位移
SVM算法会在训练过程中学习w和b的最优值。
非线性SVM与核技巧
Scatter plot with non-linear SVM decision boundary, showing classes, support vectors, and margins
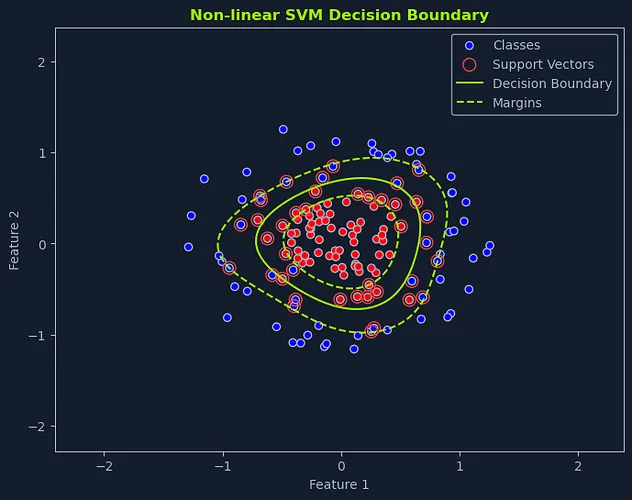
在现实世界的许多场景中，数据并非线性可分的。这意味着我们无法绘制一条直线或超平面来完美分离不同类别。在这种情况下，非线性SVM就派上用场了。
核方法原理
非线性SVM使用一种被称为核技巧的技术。这包括使用核函数将原始数据点映射到更高维的空间，在这个空间中，数据点变得线性可分。
想象将桌上的红色和蓝色混合弹珠分开的情景。如果这些弹珠混合成复杂的图案，你可能无法画出一条直线将它们分开。但是，如果你能将一些弹珠从桌面上抬起（移动到更高维度），也许就能找到一个平面将它们分离。
这就是核函数的精髓所在。它将数据转换到高维空间，在这个空间中可以找到线性超平面。当映射回原始空间时，该超平面对应于非线性决策边界。
核函数类型
非线性SVM中常用的核函数包括：
- 多项式核：该核引入多项式项（如x²、x³等）来捕获特征之间的非线性关系。这相当于在决策边界上添加曲线。
- 径向基函数（RBF）核：该核使用高斯函数将数据点映射到高维空间。它是最流行、最通用的核函数之一，能够捕获复杂的非线性模式。
- Sigmoid核：该核类似于逻辑回归中使用的sigmoid函数。它通过将数据点映射到具有S形决策边界的空间来引入非线性。
核函数的选择取决于数据的性质和模型所需的复杂程度。
图像分类应用
非线性SVM在图像分类等应用中特别有用。图像通常具有线性边界无法分离的复杂模式。
比如，想象对猫和狗图像进行分类的情况。特征可能包括毛发纹理、耳朵形状和面部特征。这些特征通常具有非线性关系。配备适当核函数的非线性SVM能够捕获这些关系，有效地将猫图像和狗图像区分开来。就像在渗透测试中使用训练良好的验证码识别模型那样，能够处理复杂的视觉模式识别任务。
SVM优化函数
要找到最佳超平面，需要解决一个优化问题。这个问题可以表述为：
- w是定义超平面的权重向量
- xi是数据点i的特征向量
- yi是数据点i的类别标签（-1或1）
- b是偏置项
这种方法的目标是最小化权重向量的大小（使边距最大化），同时确保所有数据点都能正确分类，边距至少为1。
数据假设条件
SVM对数据的假设要求很少：
- 无分布假设：SVM对数据的基础分布不做强烈假设
- 处理高维数据：它们在高维空间中表现出色，即使在特征数量大于数据点数量的情况下
- 异常值鲁棒性：SVM对异常值具有相对较好的鲁棒性，它专注于最大化边距，而非完美拟合所有数据点
SVM是一种功能强大、用途广泛的算法，已在各种机器学习任务中证明其有效性。SVM处理高维数据和复杂非线性关系的能力，使其成为解决具有挑战性的分类和回归问题的重要工具。
