type
status
date
slug
summary
tags
category
icon
password
Description
SARSA 算法
SARSA 是强化学习里的一位“老朋友”，名字来自它的五步循环：状态 State → 动作 Action → 奖励 Reward → 新状态 State' → 新动作 Action'。也就是大家常说的 S-A-R-S-A 五连击。和它的“表亲” Q-learning 一样，SARSA 也不需要环境模型，靠和环境“正面刚”来学策略，但两者在更新方式上的一丢丢差异，会直接影响到学习风格：一个更保守、更贴当前策略；一个更激进、更奔向最优。
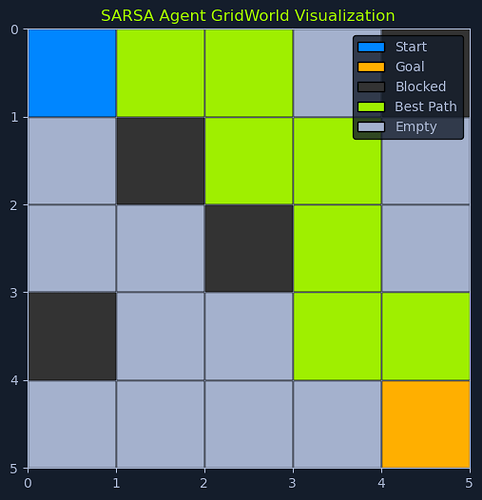
SARSA vs. Q-learning：同门不同派
- SARSA 属于“按策略”（on-policy）学习：下一步用的就是当前策略真的会选的那个动作 a' 来更新。
- Q-learning 是“离策略”（off-policy）学习：直接抄近道，用下一状态里“看起来最牛”的最大 Q 值 max_a Q(s', a) 来更新。
因此，SARSA 更新看重“我现在这套打法”会带来的长期回报；Q-learning 更像是“理想主义选手”，无视当前打法，直奔理论最优。一个稳，一个猛。很多需要稳当不翻车的场景里，SARSA 的风格更吃香。
核心更新公式（换个说法）
在任意状态-动作对 (s, a) 上，SARSA 的增量式更新为：
Q(s, a) ← Q(s, a) + α × [r + γ × Q(s', a') − Q(s, a)]
其中：
- s 是当前状态，a 是当前采取的动作
- r 是即时奖励，s' 是转移后的状态，a' 是在 s' 下按“当前策略”挑的动作
- α 是学习率，γ 是折扣因子
这一项 Q(s', a') 明确把“下一步按当前策略实际会做什么”考虑进来，于是学到的是“这套策略本身”的价值评估。
一个直观小剧场
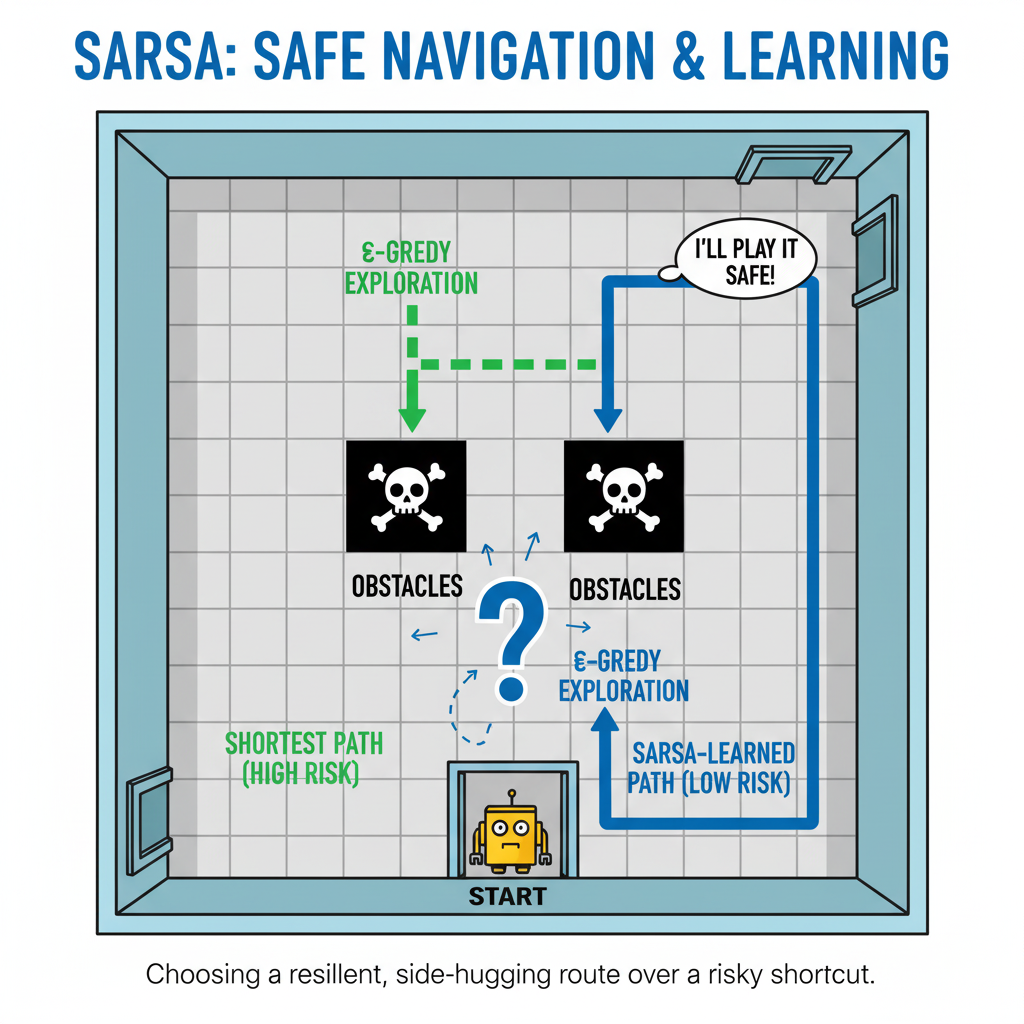
想象有个小机器人要穿越一个摆着障碍的房间。用 SARSA，它不会只看下一步哪条路名义上最短，而是会把“我现在这套走法下一步真的会怎么走”算进去。这样一来，它更倾向于学会“稳稳避坑”的路线，哪怕有些看起来很诱人的捷径因为风险大而被回避——安全第一，懂的都懂。
On-Policy 与 Off-Policy：两种学习范式
强化学习流程图：按策略（on-policy）学习基于当前策略更新，并包含探索性行为。离策略（off-policy）学习独立于当前策略，可以利用来自不同策略的数据。
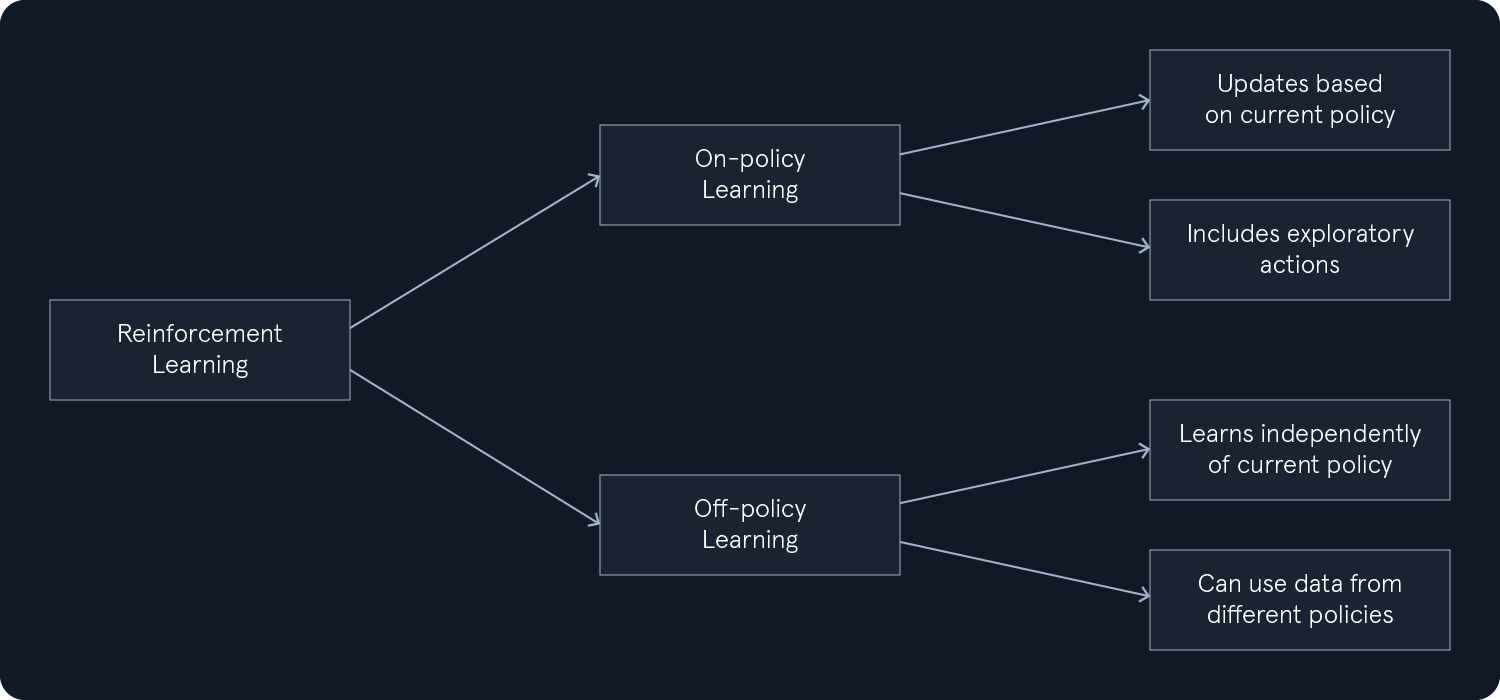
强化学习里，按策略（on-policy）与离策略（off-policy）的区别，核心在于“用谁的数据、按照谁的决策原则来学”：
- 按策略：用自己当前策略生成的数据来评估自己。包括探索时做过的那些“试错步”，统统记账。
- 离策略：学习的目标可以和收集数据的策略不一致。可以拿别的策略的数据（甚至历史日志）来学“最优解”。
从状态-动作对开始。选择 SARSA 来遵循当前策略，或选择 Q-learning 来执行贪婪最优动作。这两种方法都更新 Q 值。主要区别在于：Q-learning 旨在学习最优策略，而不考虑探索，而 SARSA 则侧重于保持当前策略的稳定性。
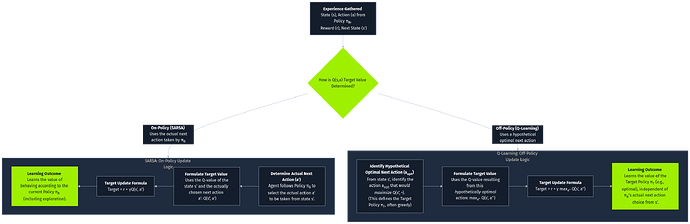
把这事儿落到具体：
- SARSA 用的是“下一步真实会做的动作 a'”，因此它评估的是“当前策略的价值”。探索行为也在账本里，学到的 Q 值天然就包含了探索与利用的平衡。
- Q-learning 则用“贪心的最大值”替代真实 a'，天然更冲向最优，但也更容易在探索时做出冒进决策。
结论直白点：要稳当与可控，优先 SARSA；要冲绩效和上限，Q-learning 常常更香，但要小心翻车风险。
探索 vs. 利用：怎么拿捏这个度
和 Q-learning 一样，SARSA 也得在“多试试新招”和“用好现有强项”之间找平衡。策略怎么选，直接影响学习速度、稳定性与最终策略质量。
ε-贪心（epsilon-greedy）
SARSA 步骤：使用 ε-贪婪动作选择，其中随机动作的概率为 ε，贪婪动作的概率为 1-ε。观察下一个状态和奖励，重复 ε-贪婪选择，更新 Q 值，结束步骤。
套路很简单：
- 以 ε 的概率随便试一个动作（探索）
- 以 1−ε 的概率选当前 Q 值最高的动作（利用）
在 SARSA 里，用 ε-贪心等于承认“探索这件事本身也会发生”，因此更新时会把这些探索步的后果一起学进去。结果就是：探索不至于太野，整体更谨慎。
Softmax（温柔一点的随机）
SARSA Softmax 步骤：从Softmax动作选择开始，计算动作概率，选择动作，观察下一个状态和奖励，重复Softmax选择，更新Q值，结束步骤。
Softmax 根据每个动作的 Q 值“按比例分配概率”：Q 越高，出场率越大，但不是一刀切地只选最大值。好处是探索更丝滑，次优动作也能偶尔上场，博一博可能出现的更优路径。
怎么选？场景优先：
- 强调安全与稳定：ε 设小点、温和探索，或者用温度较低的 Softmax。
- 强调寻优与发现：提高 ε 或 Softmax 温度，给中高 Q 的选项更多露脸机会。
收敛与参数调优：细节拉满
要把 SARSA 跑稳、跑好，两个基础旋钮很关键：学习率 α 与折扣因子 γ。
- 学习率 α：更新步子多大。α 高，学得快但可能抖；α 低，稳但慢。
- 折扣因子 γ：看多远。γ 越接近 1 越看重长远；γ 小则“眼前利益要紧”。
实践上，通常需要做些小实验来找甜蜜点。可以：
- 网格搜索不同 α、γ 组合
- 分阶段调整：前期稍大 α 促进探索，后期逐步减小稳定收敛
- 与探索策略联动：高探索搭配略保守的 α，避免震荡
关于收敛，一个常见且实用的经验是：
- 若学习率足够小且随时间衰减
- 探索机制确保每个状态-动作对会被“无限次”访问（理论上）
那么在满足马尔科夫假设的静态环境中，SARSA 可收敛到最优策略或其稳定近似。
前提假设：别忘了边界条件
SARSA 与 Q-learning 的基本假设相似：
- 马尔科夫性：下一个状态只取决于当前状态与动作。历史可以打包成当前状态本身。
- 环境静态：转移概率与奖励函数在学习期间不随时间改变。
这些前提决定了算法行为与结论的可靠性，实操里若不满足，需要做状态扩展、非平稳处理或使用更合适的方法。
一个小例子
还是回到穿越房间的机器人：
- 在门口起步，它先用 ε-贪心小试牛刀，偶尔绕开一条看起来很直的走廊去探探路。
- 如果下一步可能遇到障碍（比如中间那两块黑色格子），SARSA 的更新会把“我真的会走的那一步”考虑进去，于是学到的路线更偏向“稳妥地贴边”而不是“赌一把穿过去”。
- 结果是：路径也许不是理论最短，但更抗风险，也更符合“别碰墙”的安全诉求。
何时选 SARSA？
当你更看重“策略按现在这套打法也要稳”的时候，SARSA 很合适。它把探索行为一并纳入评估，天然偏稳，适配那些对安全性、稳定性有明确要求的应用场景。要是你追求极致最优并且能接受更激进的探索，Q-learning 也许更对味；但在一票工程场景里，“稳中求进”的 SARSA，真挺能打。
