type
Post
status
Published
date
Sep 11, 2025
slug
ai1
summary
人工智能基本概念与数学概念
tags
人工智能
category
人工智能
icon
password
Description
机器学习零基础上手指南
说到计算机科学这个大坑,人工智能(AI)跟机器学习(ML)这俩概念总是被人搞混,简直是让小白们头秃~虽说它们确实有血缘关系,但实际上各自都有独特的内涵和应用场景,理论基础也不太一样。
人工智能(AI)的奥秘
所谓的人工智能(AI),其实就是一个超级宽泛的技术领域——主要搞的就是让机器具备那些平时只有我们人类才有的智慧能力。比如说理解我们说的话、认出各种东西、做决策、解决麻烦事儿,还有从实践中吸取经验教训。这些AI系统在不同行业里都能展现出推理分析、感知判断和问题解决等超强技能。AI涵盖的核心领域主要有这么几个方向:
包括自然语言处理(NLP)让电脑读懂人话、生成文本;计算机视觉让机器拥有"火眼金睛",能看懂图片视频;机器人技术打造能独立工作或配合人类的智能机器;还有专家系统模拟行业大牛的决策思维。
- 自然语言处理(NLP):让电脑读懂、分析并生成我们的日常用语。
- 计算机视觉:赋予机器"看见"并理解图像视频内容的超能力。
- 机器人技术:研发能够独当一面或与人协作完成任务的智能机械。
- 专家系统:构建能够模仿领域专家思维决策的智能体系。
AI 最核心的使命其实不是替代我们打工人,而是增强我们的能力值。这些AI 系统的设计初衷就是提升人类的判断力和工作效率,在复杂数据分析、预测建模和重复性工作方面给我们当助手。
从医疗健康到金融投资,再到网络安全等各个领域,人工智能都能搞定那些让人头疼的复杂问题,应用场景多到数不过来。
机器学习(ML)深度解析
机器学习(ML)属于人工智能家族的重要分支,核心思想是让系统通过数据训练来提升特定任务的表现,而且不需要程序员手把手教每一步怎么做。ML算法运用各种统计方法来挖掘数据集里的规律、趋势和异常情况,让系统面对全新输入时能够进行预测、决策或分类。
机器学习按套路可以分成三大门派:
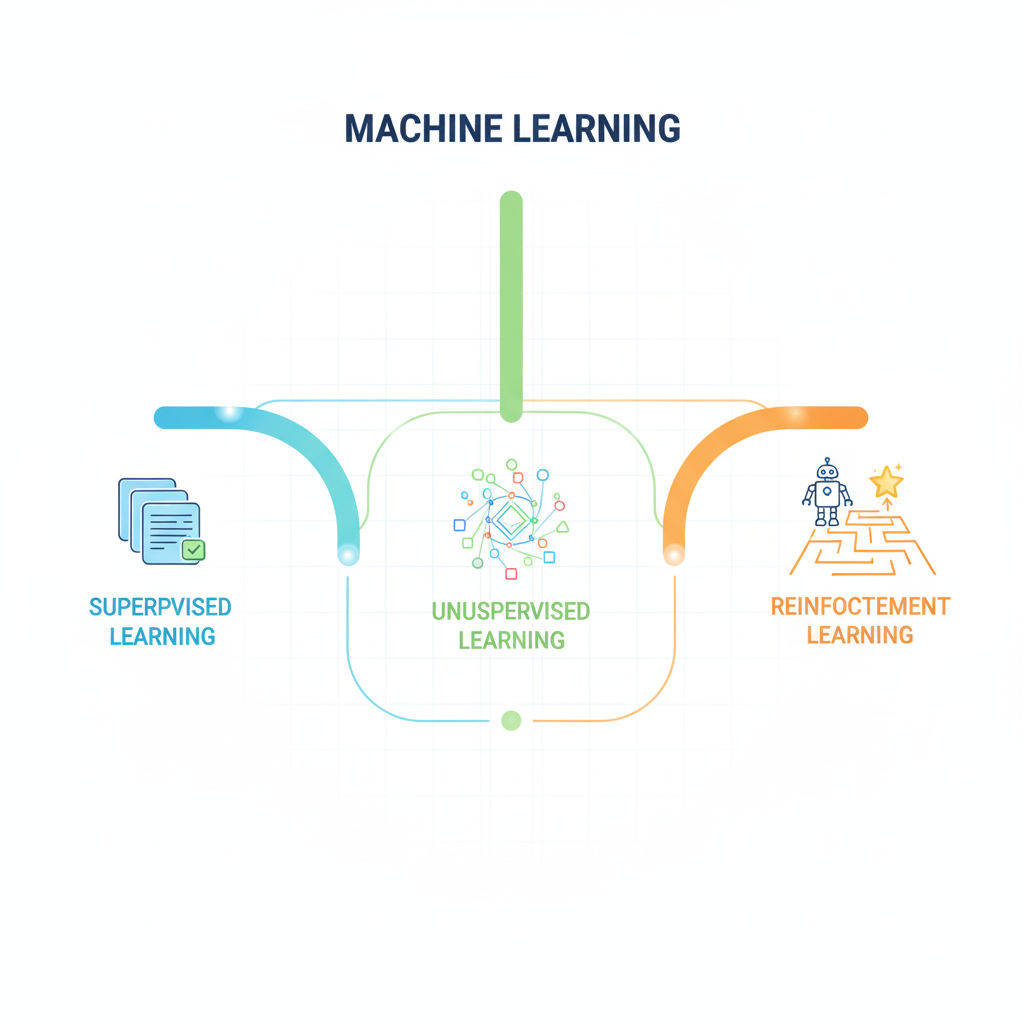
- 监督学习:算法通过带标签的训练数据来学习,每个数据样本都有对应的正确答案。典型应用场景有
- 图像识别分类
- 垃圾邮件过滤
- 金融欺诈防范


- 无监督学习:算法需要从没有标准答案的原始数据中自己摸索规律。主要用途包括
- 用户行为画像分析
- 系统异常状况监测
- 数据降维处理特别是在异常监测场景下,降维技术主要是通过减少数据特征维度来简化数据结构,让异常检测变得更加高效。
- 强化学习(Reinforcement Learning):算法像玩游戏升级一样,通过不断试错并获得奖励或惩罚反馈来优化策略。应用实例有
- 电子游戏AI
- 智能机器人控制
- 无人驾驶技术
举个栗子,假设我们用标记为"喵星人"或"汪星人"的图片数据来训练机器学习算法。通过分析这些图片的特征和规律,算法就学会了如何区分猫咪和狗狗。当它遇到一张没见过的图片时,就能根据之前学到的知识判断这是猫还是狗。
ML技术在各行各业都有超广泛的应用,主要包括
- 医疗健康领域:疾病诊断辅助、新药研发加速、精准医疗方案制定
- 金融服务行业:欺诈行为识别、风险评估建模、程序化交易策略
- 市场营销方面:客户群体细分、精准广告投放、个性化推荐算法
- 网络安全防护:威胁行为识别、入侵检测防御、恶意代码分析
- 交通运输优化:路况预测分析、自动驾驶汽车、最优路径规划
ML这个领域发展速度真的是飞快,新算法、新技术、新应用场景简直是层出不穷。它已经成为推动人工智能进步的核心引擎,为各种智能系统提供了学习进化和环境适应的核心能力。
深度学习 (DL) 技术揭秘
深度学习(DL)是ML家族中的技术新星,通过构建多层神经网络架构来从复杂数据中挖掘和提取特征信息。这些深层神经网络能够自动发现大规模数据集中的复杂模式和数据表示,在处理非结构化或高维数据(比如图像、音频、文本)的任务中表现特别优秀。

DL技术的主要特点包括
- 分层特征学习能力:DL模型能够学习层次化的数据表示结构,每个网络层都能捕获越来越抽象的特征信息。比如在图像识别任务中,浅层网络检测边缘纹理等基础特征,深层网络则能识别形状物体等高级结构。
- 端到端学习机制:DL模型支持端到端的训练方式,可以直接建立原始输入数据到目标输出的映射关系,省去了人工特征工程的复杂过程。
- 可扩展性优势:DL模型在大规模数据集和计算资源上都有很好的扩展能力,特别适合处理大数据应用场景。
DL领域常用的神经网络架构主要有
- 卷积神经网络(CNNs):专门针对图像视频数据设计,利用卷积层来检测局部特征和空间层次结构。
- 循环神经网络(RNNs):专门处理文本语音等序列数据,具有记忆功能,能让信息在时间序列中传递保持。
- Transformer架构:DL领域的最新突破,在自然语言处理任务上效果特别棒。它们采用自注意力机制来处理长距离依赖关系问题。
DL技术给人工智能的各个分支都带来了革命性变化,在以下任务中都达到了业界领先水平:
- 计算机视觉应用:图像分类识别、目标检测定位、图像语义分割
- 自然语言处理(NLP)应用:情感分析挖掘、机器翻译转换、智能文本生成
- 语音识别技术:音频转文字转录、语音合成输出
- 强化学习应用:训练智能体执行复杂任务,比如游戏对战和机器人控制
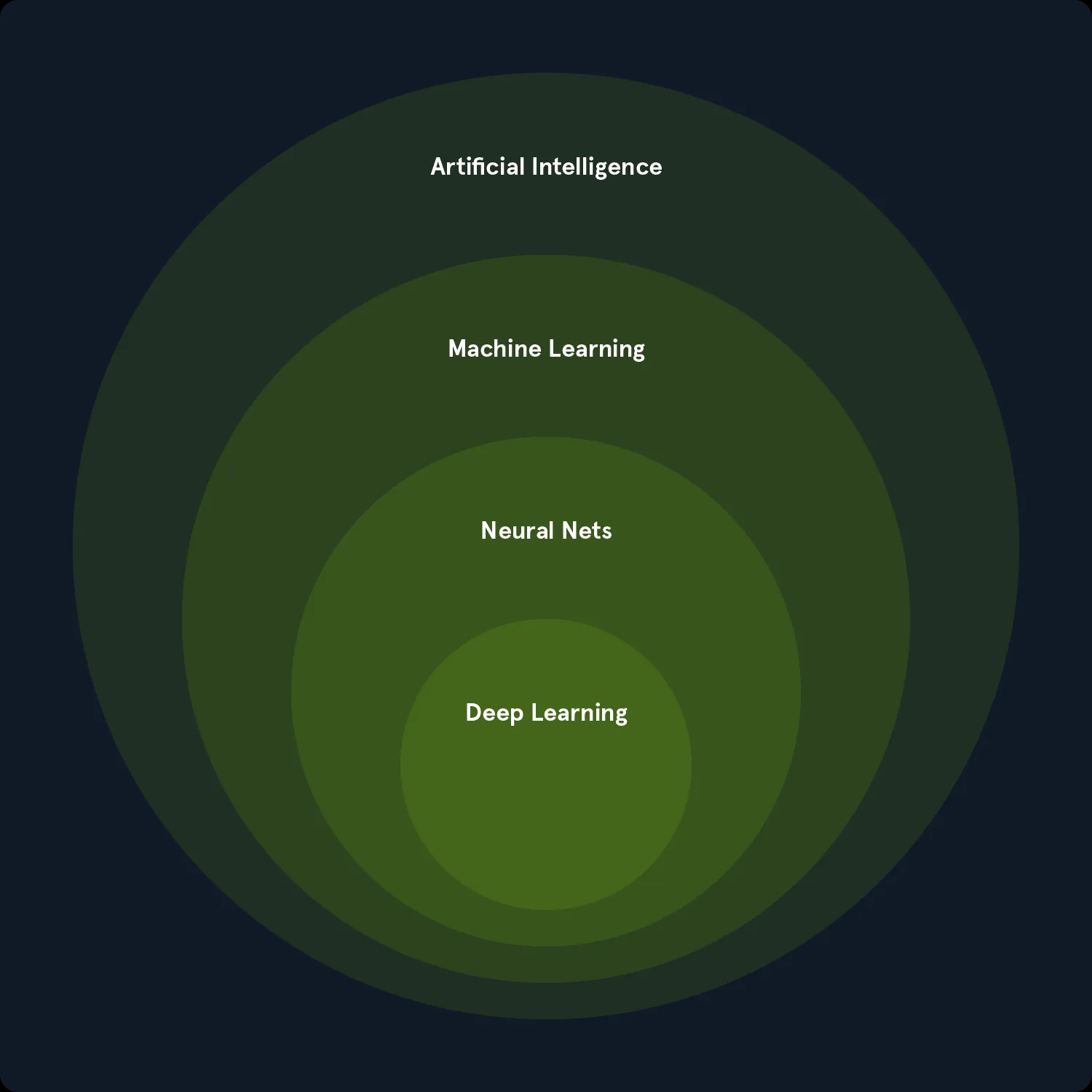
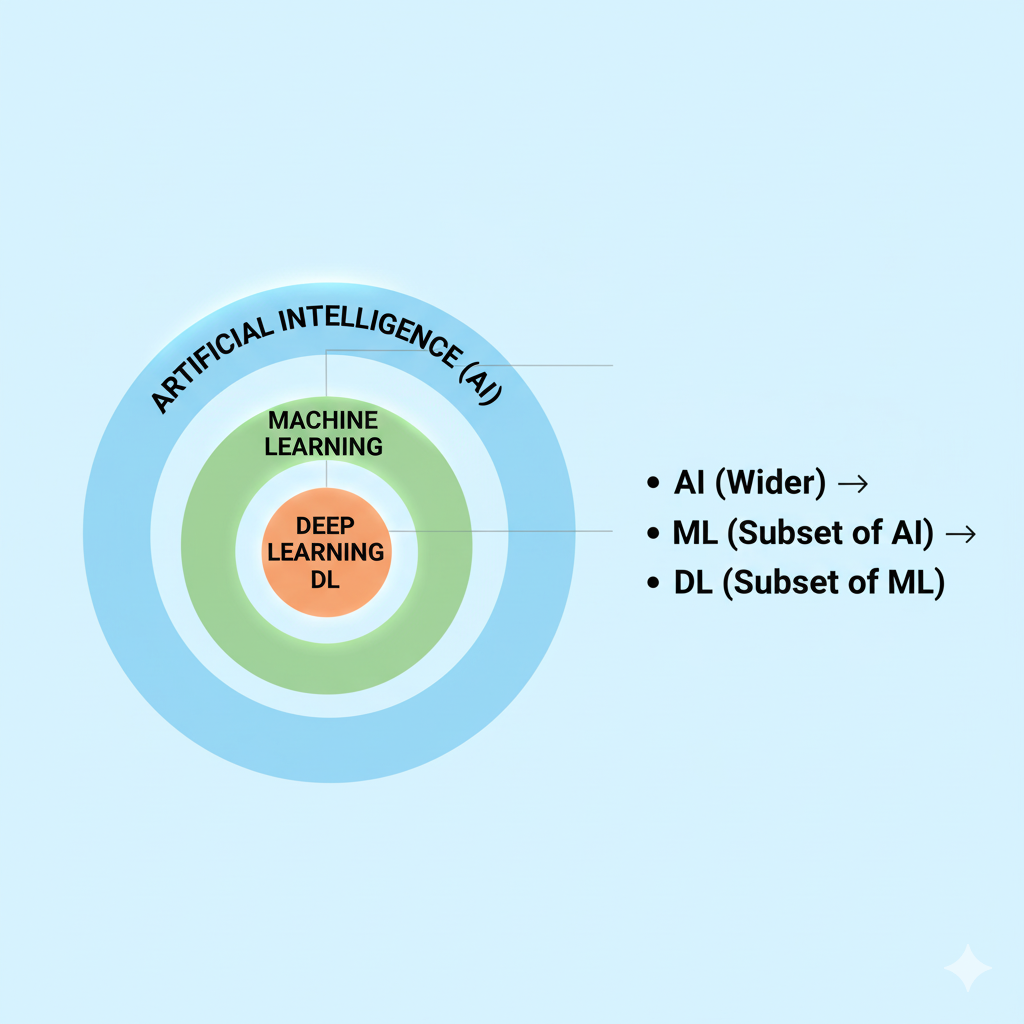
人工智能、机器学习(ML) 和深度学习( DL) 的关系网
机器学习(ML)和深度学习(DL)都属于人工智能(AI)这个大家族的重要成员,它们让系统具备了从数据中学习并做出智能决策的能力。可以说,它们是推动AI发展的核心动力,为各种智能系统提供了学习和适应环境的基础能力。
各种类型的ML 算法(当然也包括 DL 算法)让机器能够从数据中学习知识、发现隐藏模式并做出合理决策。
无论是监督学习、无监督学习还是强化学习,都在为实现 AI 的宏伟目标贡献力量。具体来说:
- 在计算机视觉领域,监督学习算法配合 深度卷积神经网络 (Deep Convolutional Neural Networks)让机器拥有了"慧眼识珠"的能力,能够精准解析图像内容。
- 在自然语言处理(NLP)方面,传统 ML 算法与先进 DL 模型(如Transformer架构)强强联合,让机器理解和生成人类语言,催生了聊天机器人和翻译软件等神奇应用。
DL 在特征提取和表示学习方面提供了超强工具,特别是在处理复杂非结构化数据的场景下,极大地增强了 ML 的整体实力。
ML、DL 和 AI 三者之间的协同效应,在它们联手攻克复杂问题的过程中表现得淋漓尽致。举几个例子:
在自动驾驶这个超级工程中,ML 和 DL 技术珠联璧合,能够处理各种传感器数据、识别路况物体并做出毫秒级决策,让汽车能够安全自主导航。在机器人应用领域,强化学习算法(通常结合 DL 技术进行增强)能够训练机器人在复杂多变的环境中执行各种高难度任务。
ML 和 DL 为 AI 的学习、适应和进化能力提供了无限可能,未来的发展前景一片光明。
人工智能中的数学
基本算数运算
乘法 ()
乘法运算符表示两个数字或表达式的乘积。例如
除法 (/)
除法运算符表示一个数字或表达式除以另一个数字或表达式。例如
加法 (+)
加法运算符表示两个或两个以上数字或表达式的和。例如
减法 ()
减法运算符表示两个数字或表达式之间的差值。例如
代数符号
下标符号(x_t)
下标符号表示以 t, 为索引的变量,通常表示序列中的特定时间步或状态。例如
上标符号(x^n)
上标符号用于表示指数或幂。例如
这种符号用于多项式表达式和指数函数。
范数(||...||)
范数是数学中的一个概念,用于衡量向量的大小或长度。在多项式表达式和指数函数中,范数用来描述这些表达式的特性。最常用的规范是欧氏规范,其计算方法如下:
范数有多种用途,例如测量向量之间的距离、正则化模型以防止过度拟合,以及对数据进行正则化处理。
求和符号 (Σ)
求和符号表示一系列项的和。例如
这表示项 a_1、a_2、...、a_n 的和 。求和在许多数学公式中都会用到,包括计算均值、方差和数列。
以2为底的对数 (log2(x))
以2为底的对数是x以2为底的对数,常用于信息论中测量熵。例如:
对数因其在减少大数和处理指数增长方面的特性而被用于信息论、密码学和算法中。
自然对数 (ln(x))
自然对数是以 e (欧拉数)为底的 x 的对数。例如
由于自然对数的平滑性和连续性,它被广泛应用于微积分、微分方程和概率论中。
指数函数 (e^x)
指数函数表示欧拉数 e 升为 x 的幂。例如
指数函数用于模拟增长和衰减过程、概率分布(如正态分布)以及各种数学和物理模型。
指数函数(以二为根 2) (2^x)
指数函数(以二为根 2) (2^x)表示将 2 提升到 x 的次方 ,常用于二进制系统和信息度量。例如
该函数用于计算机科学,尤其是二进制表示法和信息论。
矩阵和矢量运算
矩阵-矢量乘法 (A * v)
矩阵-矢量乘法表示矩阵 A 与矢量 v 的乘积。例如
这种运算是线性代数的基本运算,在各种应用中都有使用,包括变换向量、求解线性方程组和神经网络。
矩阵-矩阵乘法 (A * B)
矩阵-矩阵乘法表示两个矩阵 A 和 B 的乘积。例如
这种运算用于线性变换、解线性方程组和深度学习中的层间运算。
转置 (A^T)
矩阵A的转置用A^T表示,并交换A的行和列。例如:
转置用于各种矩阵运算,例如计算点积和为某些算法准备数据。
逆矩阵 (A^{-1})
矩阵
A 的 逆矩阵用 A^{-1} 表示,是与 A 相乘后得到同一矩阵的矩阵。例如逆运算用于求解线性方程组、逆变换和各种优化问题。
行列式 (det(A))
一个矩阵 A的行列式是一个可以计算出的标量值,它在各种矩阵运算中被使用。例如
行列式决定了矩阵在计算体积、面积和几何变换时是否可逆(行列式不为零)。
迹(tr(A))
在数学中,迹通常指的是方阵主对角线元素的和,用于确定矩阵是否可逆(行列式非零)。在计算体积、面积和几何变换时,迹是一个重要的概念。
迹线用于各种矩阵属性和计算特征值。
集合论
基数 (|S|)
基数表示集合 S 中元素的个数。例如
基数用于元素计数、概率计算和各种组合问题。
并集(∪)
两个集合 A 和 B 的 并集 是 A 或 B 或两者中所有元素的集合。例如
并集用于组合集合、数据合并以及各种集合操作。
交集 (∩)
两个集合
A 和 B 的 交集是 A 和 B 中所有元素的集合。例如交集可查找共同元素、进行数据筛选和各种集合操作。
补集 (A^c)
集合A的补集是不在A中的所有元素的集合。例如
补集在集合运算、概率计算和多种逻辑运算中都有应用。
比较运算符
大于或等于 (>=)
大于或等于运算符表示左边的值大于或等于右边的值。例如
小于或等于 (<=)
小于或等于运算符表示左边的值小于或等于右边的值。例如
等于 (==)
等于运算符检查两个值是否相等。例如
不等于 (!=)
不等于运算符检查两个值是否不相等
特征值和标量
Lambda (特征值) (λ)
lambda 符号通常代表线性代数中的特征值或方程中的标量参数。例如
特征值用于了解线性变换、主成分分析 (PCA) 和各种优化问题的行为。
特征向量
特征向量是一个非零向量,当与矩阵相乘时,其结果是自身的标量倍数。标量就是特征值。例如
特征向量用于了解数据中方差最大的方向、PCA 等降维技术以及各种机器学习算法。
函数和运算符
最大值函数 (max(...))
最大值函数从一组值中返回最大值。例如
最大值函数用于优化、寻找最佳解决方案以及各种决策过程。
最小函数 (min(...))
最小值函数从一组值中返回最小值。例如
最小函数用于优化、寻找最佳解决方案以及各种决策过程。
倒数 (1 / ...)
倒数倒数表示 1 除以表达式,有效地反转了数值。例如
倒数用于各种数学运算,如计算速率和比例。
省略号 (...)
省略号表示模式的延续或序列的继续,通常用来表示不确定或持续变化的过程。例如:
省略号在数学符号中用来表示序列和数列中间不确定或持续变化的数值。
函数与概率
函数表示符号 (f(x))
函数表示符号表示以x为变量的函数f 。例如
函数符号用于定义数学关系、模拟现实世界的现象以及各种算法。
条件概率分布 (P(x | y))
条件概率分布表示在给定y的情况下x的概率分布。例如:
条件概率用于贝叶斯推理、不确定情况下的决策以及各种概率模型。
期望运算符 (E[...])
期望运算符表示随机变量的期望值或其概率分布的平均值。例如
期望值用于计算平均值、不确定情况下的决策以及各种统计模型。
方差 (Var(X))
方差测量随机变量 X 围绕其均值的扩散。计算公式如下
方差用于了解数据的分散性、评估风险和使用各种统计模型。
标准差 (σ(X))
标准差是方差的平方根,是随机变量离散程度的度量。例如
标准差用于了解数据的分布、评估风险和使用各种统计模型。
协方差 (Cov(X, Y))
协方差测量两个随机变量 X 和 Y 的变化情况。计算公式如下
协方差用于理解两个变量之间的关系、投资组合优化和各种统计模型。
相关系数 (ρ(X, Y))
相关系数是一种归一化的协方差度量,范围从-1到1。它表示两个随机变量之间线性关系的强度和方向。例如:
在数据分析和各种统计模型中,相关系数用于理解变量之间的线性关系。






